まずはサイコロの実験から
ギャンブルと言えば、サイコロ。吉田拓郎の「落陽」という歌で、おっちゃんがくれたアレです。(昭和歌謡です。知らない方スンマセン)
サイコロって、1〜6の目が均等に出現する代表格ですよね。コンピュータの疑似乱数を使って、1000回サイコロを振った結果のヒストグラムを作ってみました。
サイコロを1つ、1000回振ったときの目の分布
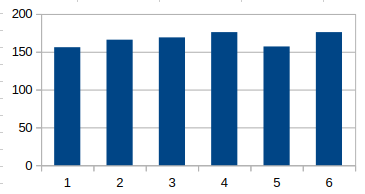
疑似乱数なので多少のバラツキは目をつぶるとして、一様分布であることはわかりますよね。実際のサイコロもこれぐらいはブレると思います。ピッタリ揃う方が不自然です。昔の研究者は、真面目にサイコロを振って、実験したんだろうなぁ。
サイコロを2個振って、出た目の平均を求めてみる。(1000回試行)
次に、サイコロを2つ振った場合。合わせて2〜12の目になる。平均は3.5ですよね。なんかイビツだけど、正規分布に似てる?似てない?って感じですね。
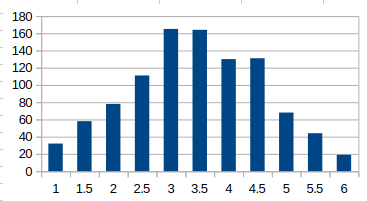
サイコロを5個振って、出た目の平均を求めてみる。(1000回試行)
サイコロを5個に増やして、平均値を出してみよう。まだちょっとイビツだけど、なんとなく正規分布に似てきたような気がしませんか?
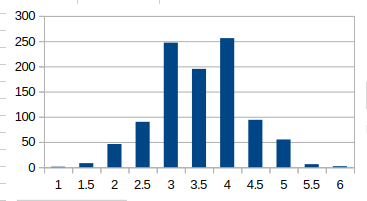
サイコロを10個振って、出た目の平均を求めてみる。(1000回試行)
どんどん増やしてみましょう。次は10個です。これは綺麗な釣鐘型ですね!ただ、1, 5.5, 6のデータは0でした。全体的にシュッと細くなった感じがしませんか?
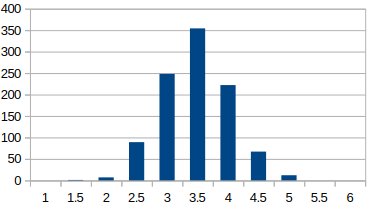
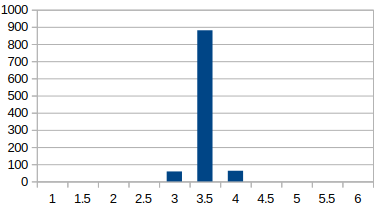
サイコロを100個振って、出た目の平均を求めてみる。(1000回試行)
まぁ、Perlスクリプトで実験すると、1秒もかからず結果が出るんですけど、、、昔の人は手作業で実験したんですよね。ご苦労さまです。
なんと、1000回施行してもデータは3, 3.5, 4 しかありませんでした。しかも、かなり細くなりましたね。
実はこれらの実験結果が、「大数の法則」と「中心極限定理」そのものなんです。
大数の法則とは
Wikipediaから引用すると、以下のような小難しい説明が書かれてますね。
大数の法則(たいすうのほうそく、英: Law of Large Numbers, LLN)とは、確率論・統計学における基本定理の一つ。公理的確率により構成される確率空間の体系は、統計学的確率と矛盾しないことを保証する定理である。
たとえばサイコロを振り、出た目を記録することを考える。この試行回数を限りなく増やせば、出た目の標本平均が目の平均である 3.5 の近傍から外れる確率はいくらでも小さくなる。これは大数の法則から導かれる帰結の典型例である。より一般に、大数の法則は「独立同分布に従う可積分な確率変数列の標本平均は平均に収束する」と述べられる。
正規分布していない一様分布のサイコロであっても、限りなく試行回数を増やせば、得られる結果は理論的な平均値「3.5」に限りなく近づくわけですね。これまでの実験結果そのものです。
中心極限定理とは
同じように、こちらもWikipediaから引用してみます。小難しいことが書いてますね。
中心極限定理(ちゅうしんきょくげんていり、英: central limit theorem, CLT)は、確率論・統計学における極限定理の一つ。大数の法則によると、ある母集団から無作為抽出した標本の算術平均は、標本の大きさを大きくすると母集団の母平均に近づく。
これに対して中心極限定理は、標本の算術平均と母平均との誤差の確率分布が、定理の条件が満たされれば、標本の大きさを大きくすると近似的に期待値ゼロの「正規分布」になることをいう。
なお、母集団の分散が存在しないあるいは有限の実数にならないときには、標本平均と母平均の誤差の分布の極限が正規分布と異なる場合もある。(上手く行かない場合もあるよと言うこと。)
中心極限定理は、統計学における基本定理であり、例えば世論調査における必要サンプルのサイズの算出等に用いられる。
つまり、「何本の木を確認したら(サンプルサイズ)、森全体の状態をある程度正確に予測できるか」に使えるわけですね。
もちろんこれはパラメトリック(四則演算可能なデータ)である場合に限った話です。アンケートの意識調査のようなノンパラメトリックなデータは別です。(これは別の記事で説明します。)
アンケートで「好き・嫌い」等の印象を5段階評価して、平均値を出したり、結果をT検定したりしている研究が何と多いことか。ダメですよ!!好きにも色々レベルがあるでしょ。平均値は意味がないんです。
一応、定理の部分もWikipediaから引用します。何言ってるかわからないでしょ。

要点は、
母集団の分布がどんな形であれ(サイコロのような一様分布であっても)、そこから標本を沢山集めて平均値を求めた場合、母集団の平均値は標本平均と同じ。
母集団から得られた標本の平均値の分散は、母集団の分散σ2 をサンプル数nで割ったもの(σ2/n)になります。しかも正規分布してます。
という事です。サンプル数nで割ってるので、nを増やすと分散値が小さくなるわけですね。
(数学的証明手順は、Wikipediaを読んでね!😅)
大いなる矛盾からT分布の発見へ・・・・
ここで大いなる矛盾に気づきませんか?
そもそも母集団の分散σ2は、どのようにして知れば良いのでしょう。一般的には不偏分散(分散をnではなくn-1で割ることで、イイ感じに補正したアレ)を使うしか無いんですが、、、ホントに大丈夫?
それに沢山のサンプルが必要って、、、サンプルが沢山集まらなければ統計処理出来ないの? 実際、使えねぇ!
実は、これらの疑問に気がついた若者がいたんです。ウィリアム・シーリー・ゴセットという若者で、ギネスビールの品質管理をしていた技師だったようです。彼はこれらの問題を解決する「T分布」を考案しました。ギネスビールでは秘密保持のため従業員による科学論文の公表を禁止していたので、彼はこの問題を回避するため「スチューデント」というペンネームを使用して1908年に論文を発表しました。
天才っていつの世にも居るんですね。
ただ、あまりにも複雑な補正式の塊で、当時のゴゼットの師匠であるピアソン先生も、発表当時は誰もその論文の重要性に気づかなかったようです。
その後、ロナルド・フィッシャーがこの論文の重要性を見抜き、ペンネームの「スチューデントのt分布」と呼んだため、現在も、このように呼ばれるようになりました。流石!天才のフィッシャー先生です!😍
次回は、このT分布について詳しく解説します。超難しいですけど、興味深いですよ〜!