今回は殆どがWikipediaからの引用になってしまいますが、ご容赦ください。でも読み応えありますよ!!
T分布とは
標準正規分布は、二項分布をヒントに、釣鐘型の形を模して作られた分布であることは説明しましたよね。
大数の法則、中心極限定理にて、統計学の基礎となる分布ですが問題点がありました。
・絶対に正確に知り得ない母集団の分散σ2が必要。不偏分散を応用してよいかは議論の余地があった。
・膨大なサンプル数が必須であった。
この難題を解決したのがウイリアム・シーリー・ゴゼットです。
超簡単に言うと、「正規分布を改造して、サンプル数が少ないときには、安全域が広くなるように変形したら良いのでは?」という発想です。
νは「自由度」と呼ばれ、ν=n-1と定義されています。
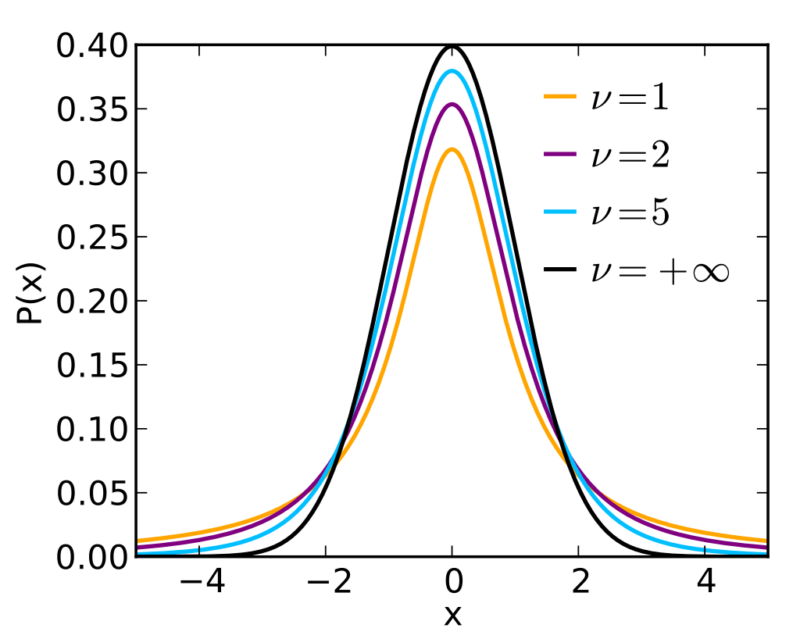
自由度1(データ数2)だと、コーシー分布と呼ばれる幅広い分布に一致します。もちろんデータ2個の研究なんてありえないのですが、、、、
自由度νが増えるに従い、分布は正規分布に近づき、ν=∞(無限大)の時に、最も細い「正規分布」に一致します。
何故n-1が自由度と呼ばれるかというと、諸説あるのですが、平均値がわかっている場合に、n-1個のデータは何であっても自由。最後の1つの数値で補正できるから。とか、不偏分散で補正する時に、データ1個分抜く。このn-1は統計の式でよく使うからν=n-1と定義したほうが、式が見やすいから。等でしょうか。(このことについては、あんまり詳しくないです。スミマセン。)
T分布の定義について(Wikipedia引用)
ウィリアム・シーリー・ゴゼットが天才過ぎて、当初、ピアソン師匠でさえも、この論文を理解できなかったのかは、その定義式を見たら理解できるかも。複雑難解です。

なお、Γ関数の定義はこちら。

わかりました?さっぱりわかりませんよね! でも大丈夫です。現代ではコンピュータが一瞬で計算してくれます。
T分布の原理(自由度で変形する分布)という所だけ、まずは理解してください。
T分布の発見によって、ある程度少ないサンプルであっても、不偏分散(サンプルから導出された母分散の推定値)を使って統計処理出来るようになったわけです。
ただし、処理できるのは「平均値の区間推定」のみであり、「母集団が正規分布していることが前提」になります。 ←【ここがめっちゃ重要です!!】
ウィリアム・シーリー・ゴセット(William Sealy Gosset)の生涯(Wikipedia要約)
ゴゼットは、1876年6月13日に、イギリス イングランド、ケント、カンタベリーに生まれました。
オックスフォード大学ニューカレッジで化学と数学を学んだとのこと。やはり天才ですね。
1899年にギネスビール社のダブリン醸造所に就職し、統計学の知識を醸造と農業(オオムギの改良)の両方に応用しながら実地の研究を重ねたようです。
1906年から1907年にかけてカール・ピアソンの研究室で研究しています。ギネスビール社では企業秘密の問題で社員が論文を出すことを禁止していたので、ゴセットは Student(スチューデント)というペンネームで1908年に論文を発表しました。従って、この彼の最も有名な業績は「スチューデントのt分布」と呼ばれることになります。
当初、ピアソン師匠は、これを重視していなかったようです。この論文は醸造技術者が関心を寄せる小標本の問題(サンプル数はあまり多くできないが、なるべく正確な答を得たい)に応えるものだったが、当時の生物測定学者(ゴルトン及びピアソンら)は、「できるだけ多くの測定を行って正確な答を求めることを重視していた」からのようです。まぁ、コンピュータの無かった時代に、補正に補正を重ねた複雑怪奇な分布式を直ちに理解しろというのがそもそも難しいわけですし、かの有名なピアソン先生の理解を超える難解な論文だったというわけですね。
ただ、完全に無視したわけではなく、1908年の「平均値の誤差の確率分布」(The probable error of a mean)を初めとして、ほとんどの論文がピアソンの主宰する "Biometrika" 誌に発表されたようです。「よくわからんけど、雑誌には載せてあげてた」ということなのかな?
ゴセットは、1935年にダブリンからロンドンに新しく造られた醸造所に移り、その2年後の1937年に61歳でその生涯を閉じたようです。昔の人は亡くなるのが早いよねぇ。
ピアソンとフィッシャーとの関わり(Wikipedia要約)
ゴセットによる小標本研究の重要性を見抜いたのはピアソンではなく、ロナルド・フィッシャーでした。ゴセットの見出した統計量に t という記号を充てた現在のシンプルな形に整えたのもフィッシャーです。また、t分布を回帰分析に応用したのもフィッシャーです。流石、天才は違うね!
ピアソンとフィッシャーは論敵というべき仲だったようですが、ゴセットは穏やかな人柄で、両者との交友関係を保ち続けたと言われています。
今日はここまで。次は「推定」ついて、臨床検査の基準範囲を例に述べたいと思います。
(Wikipediaから引用)
