統計学って聞くと、殆どの方が「苦手~」「わからない!」「パス!」って思うのでは。特に数学が得意な人程、統計学は躓きやすいですね。かつての僕のように。
僕は皆さんに、統計を好きになってもらいたい。そういう気持ちを込めて記事を書こうと思います。
統計学を理解するメリット(デメリットは無い)
統計学を理解すると「他人に騙されなくなる!」唯一無二のメリットですね。全ての科学論文が、実験結果を統計学的に処理し吟味し、結論を導き出します。統計を理解することは、全ての学問の基礎を学ぶことになるんです。
逆に統計を理解していないと、真実なのか否か、理解する力が付かないんですよ。
ぶっちゃけ統計は「無謀なことをしている学問」なんです
「木を見て森を見ず」って諺、聞いたことありますよね。木ばかり見ていると、森全体の状態を見失う。やってはいけない代名詞的なことわざです。医学の世界でも「病気ばかり診て、人を診ないのは、医師として失格だ!」と先輩に教わります。(特に精神医学においては、患者を取り巻く環境を診ずに診断や治療をすると、とんでもない失敗をします。)まぁ、それは置いておいて。
要するに、統計学は「木を見て、森を予測する」学問なんです。所詮、無謀なことにチャレンジしているわけです。難しくて、理解不能で当たり前。まだまだ未完成の学問です。どんどん進化しています。
だから、「いったい何本の木を、どのようにサンプリングするのか。それに見合うコストは?判断基準(エンドポイント)は?」ということが、研究ではとても重要なのです。現代では計算はコンピュータがやってくれます。研究は研究デザインが全てと言って過言ではありません。このことを、まず肝に銘じてください。
稀に統計の先生でも、このことを理解しないまま技術論だけ教えようとする人が居ます。だから生徒は統計学に苦手意識を持ってしまうんですよね~。
まずは、ギャンブルの話をしよう。
かたい話は、これくらいにいして。皆さんコイントス知ってますか? 知ってますよね!(正しいコインであれば)表と裏が2分の1の確率で出るアレです。サッカーで最初にボールを蹴る側を決めるときにも使いますよね。
「順列」と「組み合わせ」を知ろう(これが分からないと、コイントスの話が出来ない)
まずは「順列」から。ちょっと難しいけど頑張って!
A,B,C 3人の学生がいて、リレーを走る順番の組み合わせって、いくつあるか数えられますか?
「ABC」「ACB」「BAC」「BCA」「CAB」「CBA」の6通りです。
考え方としては、まず3人の内の1人を選んで、次に2人の1人を選びます。最後の1人は自動的に決まりますね。3x2x1=3! (3の階乗)になっているんです。4人だったら4!、10人だったら10!です。数学的に美しい!
では、次の段階へ。(ここから少し難しい)
1クラス30人の学生がいて、この中から3人を選んで、リレーを走る順番を決める場合はどうでしょうか。
これも全く同じ考え方で解けます。
30人から1人選び、29人から1人選び、28人から1人選ぶことになります。30x29x28=24,360通り。クラス対抗リレーの組み合わせってこんなに膨大になるんです。
でも皆さんは、誰がクラス代表のリレー選手で、どの順番で走るべきか直感で分かりますよね!人間の直感って凄いですね!
順列の公式は
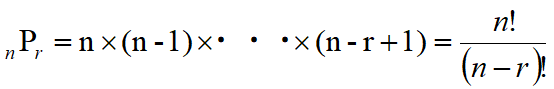
となります。30P3=30x29x28です。Pは、Permutation の頭文字ですね。
nから1ずつ減らしながらr個の数字を掛けていくと覚ると楽ですよ。
つぎに「組み合わせ」について学ぼう
順列の公式が理解出来たら、組み合わせは簡単です!
30人から3人を選ぶけど、その3人の走る順番は無視するわけですね。
30人から3人を選ぶ「順列」の公式は30P3=30x29x28でしたね。
3人の走る順番の組み合わせは3!=3x2x1ですね。
ということは、30P3を3!で割れば良いのです。(ここ重要!!!)
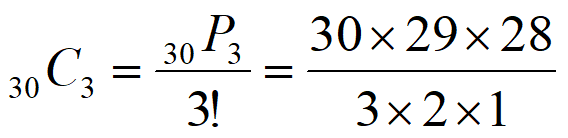
となります。
n人からr人を選ぶ組み合わせの公式は、(見た目はヤヤコシイですが)
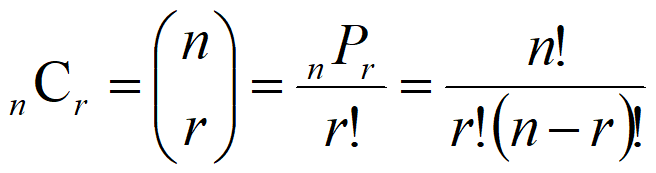
になります。順列の公式をr!で割るだけ。Cは、Combinationの頭文字ですね。
組み合わせ公式は、「分子がnからr個、分母がrの階乗」と覚えたら楽です。
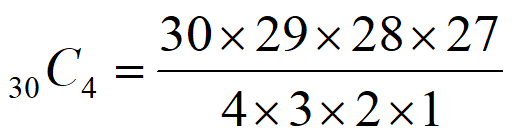
簡単ですね。
確率の計算方法を知ろう
「組み合わせ」が分かったら、次は確率の計算方法を学ぼう! 確率は、起こりえる全ての事象を分母とし、観察したい事象の数を分子にして計算します。

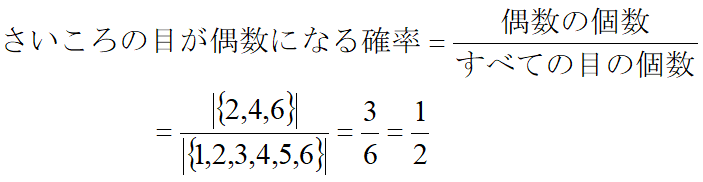
こんな感じです。そんなに難しく無いですよね。
では、さいころを10個投げて、2個だけ1の目が出る確率は、どうなるでしょうか。
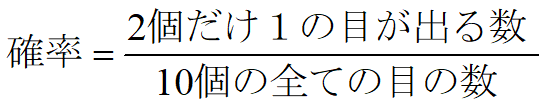
分母は、さいころ10個の目の数 = 6×6×・・・×6 = 610 になります。
分子が難しいですね。以下のように考えます。
「1の目」が2個出る組合せ = 10個のうち2個が「1」で、残り8個が「1」以外
= (10個から2個を選ぶ組み合わせ「1」)×(残り8個は「2」~「6」の5通り)
= (10C2 × 1)× 58 = 45×58
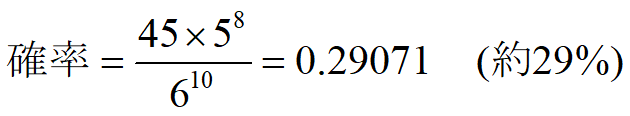
理解出来ましたか? 結構難しいですよね!😓
期待値
確率事象から計算で求められる予測値を「期待値」と言います。
例えば、袋の中に10個の玉が入っていて、3個が黒、7個が白だとします。ランダムに3個取り出すときに、2個が黒である確率はどうなるでしょう。

こんな感じで「組み合わせ」を使って計算できます。では黒玉が0個~3個になる、それぞれの期待値はどうなるかというと、
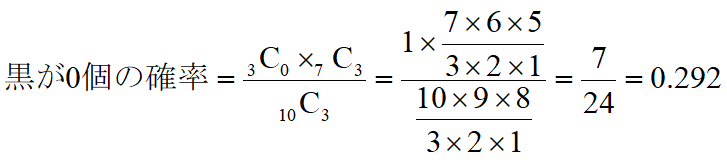
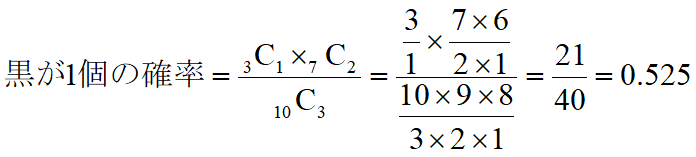
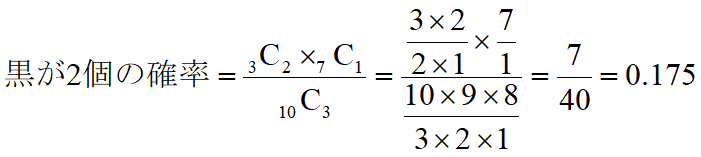
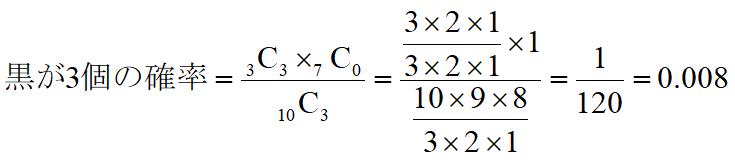
となります。これを表にまとめると下記のようになります。全ての確率の和は1になります。度数分布表に似てますね!
| 黒玉 | 確率 |
| 0 | 0.292 |
| 1 | 0.525 |
| 2 | 0.175 |
| 3 | 0.008 |
コイントス実験
実は、次女が小学校時代に夏休みの研究テーマに悩んでて、直ぐに出来て面白い実験として「10円玉10枚を投げたら、表が何枚出るのか」を研究してもらいました。
家族ぐるみでハマって100回やって、1度も全部表(または裏)は出ませんでした。

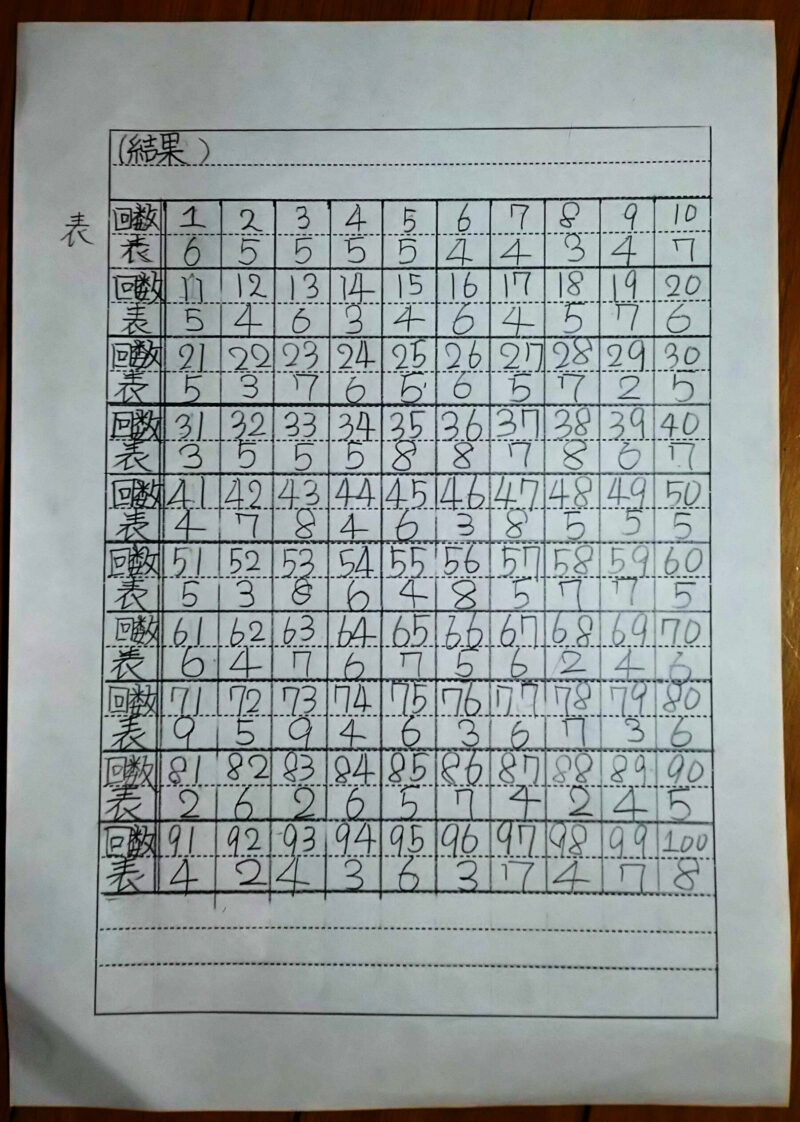

なかなか素晴らしい結果ですね!!! 綺麗な釣鐘型になっています。
ちなみに全て表または裏になる確率って、わかります?計算で求めることができます。ここで組み合わせ(Combination)の知識が必要になるんです。表計算ソフトExcel,Calcでは=COMBIN(10,0) ~ =COMBIN(10,10)で簡単に計算できます。実際に計算した結果を示します。
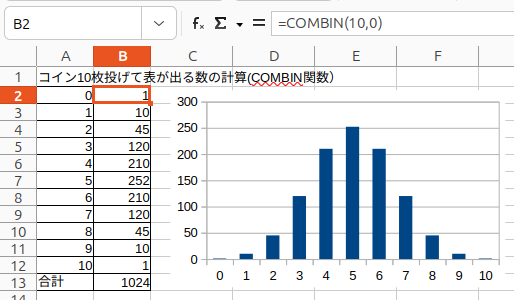
何と512回に1回の確率で全て表か裏が出ます。如何にギャンブルが無謀なことか、わかりますか?
二項分布から正規分布が発明された
コイン投げを何度も繰り返して得られるこの分布を「二項分布」と言います。コイントスのように「表・裏」の2項目から得られる分布だからです。平均値を中心に、左右対称の釣鐘型になっています。
コンピューターが無かった時代に、この二項分布を計算するのは大変骨が折れる作業でした。従って過去の統計学者は、この釣鐘型を平均値と分散値の2つのパラメーターで表現できないかと研究し、1730年にド・モアブルが二項分布のnを非常に大きくすると、正規分布の式で近似できることを発見しました。その後、ラプラスが精密化し、統計学者の中では発見者に敬意を示し、ドモアブル・ラプラスの定理と呼ばれています。
正規分布はガウス分布と呼ばれることもしばしばあります。これは18世紀から19世紀に渡って活躍した数学者C.F.ガウスに由来します。ガウスは天文学の観測データの研究から測定誤差がある法則に従うことを導き出し、誤差理論を確立しました。これが正規分布を統計学に応用した基礎となったと言われています。ガウスは自分が独自に発見したと主張したとか? まぁ、大人な事情が見え隠れしますよね。
正規分布は平均をμ、分散をσとし、次の式で表現されます。(注:式のイメージはWikipediaのものです。)
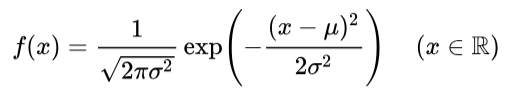
更に、平均値を0、分散値を1と定義し、最もシンプルな形にしたのが「標準正規分布」の式です。統計学の「メートル原器」みたいなものですね。
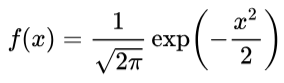
これなら手計算でも表が書けそうですね!実際に統計の教科書の巻末付録に標準正規分布の面積の表を見たことあるでしょう。アレですよ!今ならパソコンでちょちょいと計算出来ますが、昔の人は手計算で頑張ったんです!
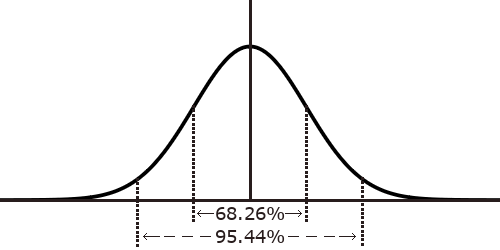
標準正規分布の特徴は、全体を積分すると面積が1であり、平均値±1SDに68.26%、±2SDに95.44%の面積が含まれます。(ピッタリ95%は1.96 SD、99%は2.58 SDになります。)
上手い事できてる式ですよね。人間が使いやすいように考案した近似式なんです。
数学が得意な人は「近似式=適当」って感じが、ピンとこないですよね。
統計学は実用化を目的に考案された学問なのです。
今日はここまで。次回は中心極限定理と信頼区間について説明します。
分かりやすく、工夫して説明します!!
(補足)平均値と分散値について
後で読み返して、SDとかサラッと説明なしで書いちゃってましたね。もしかして説明しておいた方が良いかなと思って追記しました。
「データが集中している所」に関する注意点
平均値(相加平均)は、データを全て足して、データの数で割ったものですね。数式で書くとヤヤコシイですが至ってシンプル。
小学校高学年でも理解できます。
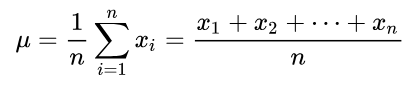
統計学では、数学的な平均の他に、標本平均と表現されるものがあります。どちらかというと、統計学で重要なのは標本平均ですね。得られたデータから計算した平均のことで、予測したい母集団の平均値と標本平均は一致します。(同じ式が使えます。)
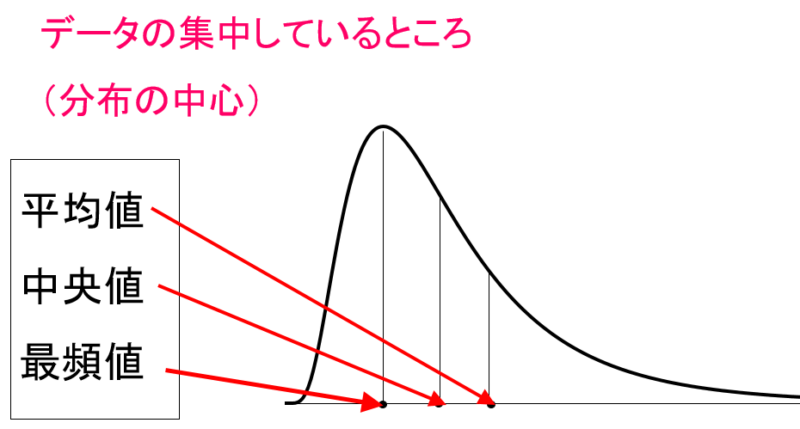
ついでに、最頻値・中央値についても、図で理解しましょう。
分布が歪んでいる場合に、平均値・中央値・最頻値にはズレが生じます。ゴミデータ(外れ値)が標本に紛れている場合等です。失敗したっていいじゃないか。人間だもの。だから、外れ値によって間違った結論を導き出さない為に、中央値、最頻値が重要になる場合があります。
データのバラつきに関する注意点
分散値については、ちょっとヤヤコシイ問題があります。まずはデータのバラつきを表現する方法について説明します。
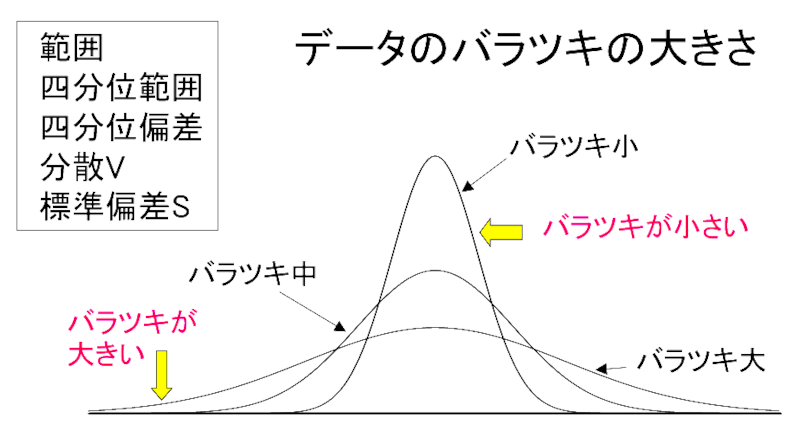
もっとも簡単なのは「範囲(Range)」ですね。単純ですが「ゴミデータ(外れ値)」に最も弱いという弱点があります。
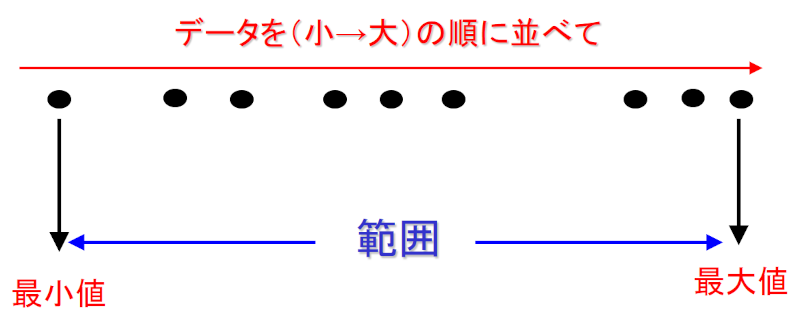
ゴミデータに強く、しかも処理が簡単なのが、四分位数(四分位偏差)です。便利ですよ。
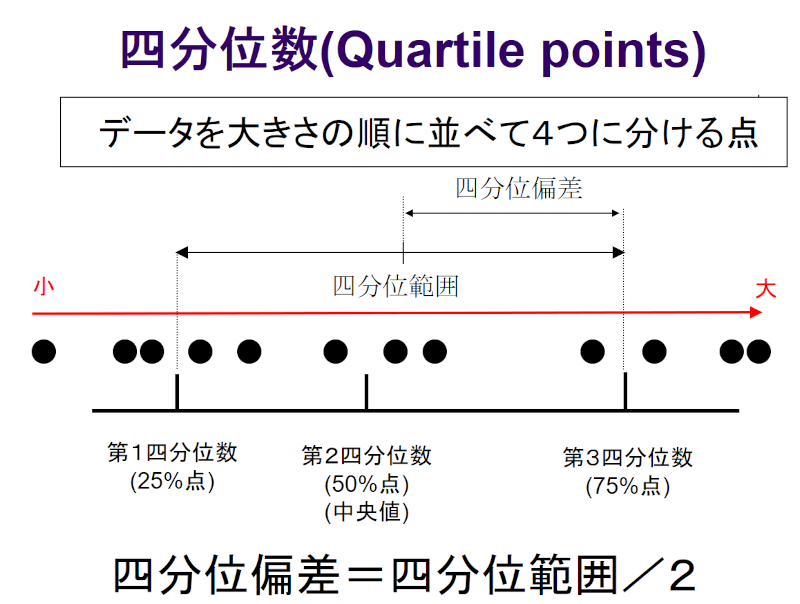
でもって、分散の式なのですが、数学的な分散の式とは別に、統計では「不偏分散」なるものが出てきます。最初の躓きポイントですね。後で詳しく説明します。
まずは数学的な分散の計算式から。数学的な分散とは、平均値からの距離の2乗を足し(「偏差平方和」と言う)、これをデータ数nで割ったものです。

図で表現すると、こんな感じです。
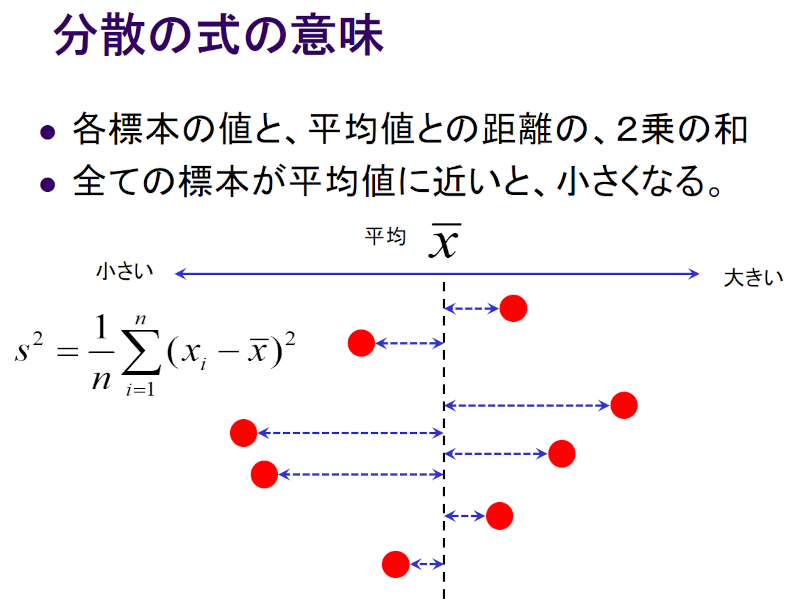
ところが、我々が手にする標本には、あるクセがあるのです。何と標本の分散値は、真の分散値よりも小さくなってしまうのです。
これは実験で証明できます。正規分布するように調整し準備したカード1000枚を準備し、これを仮の母集団とします。そこから10枚のカードを取り出して分散値を計算します。すると、どうやっても母集団の分散値よりも、値がほんの少し小さくなるのです。
そこで、nではなく、(n-1)で割ると、イイ感じになることが発見されたわけです。
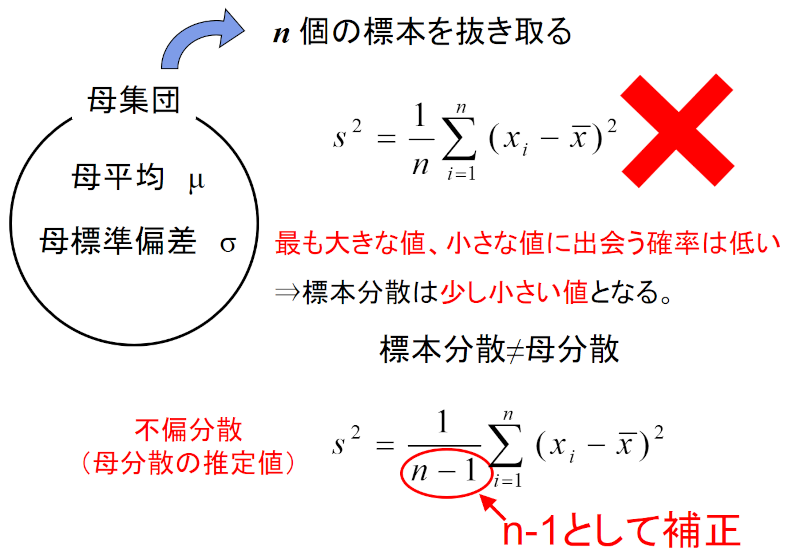
数学を愛する人が嫌悪する「補正」。そんないい加減な・・・と思うでしょうが、実験を何度も繰り返し、これで良いという結論になりました。(ただし、母集団の分布が正規分布から大きく外れている場合には、うまくいかない。世の中そんなに甘くない!)
でもって、正規分布の所で説明したSDとは、「標本標準偏差(下側の式)」になります。だって実験データはサンプルですからね。

以上、補足でした。