2025年共通テストの統計問題を解いてみる
検定の解説のネタをどうしようかと悩んでいたんですが、調度2025年度共通テストが終わり、「話題にもなるだろうし、いっちょ、この問題の解説でもしたら、バズるかな?」😆と、邪(よこしま)な気持ちで問題を読んでみました。
結論から申し上げますと、「なんじぁあ!こりぁあ!😱」、、、、全然ダメじゃん!😡
でも、もう準備したので公開します。😭
冷静に考えたら、高校の統計ではT分布まで到達してないのかもですよね。だから問題自体が、相当、伏線が張られて、吟味されてるなとは思いましたが、、、、むむむ?片側検定で有意水準5%? これが正しい検定と誤解されると、困る!!!!
2025年共通テスト問題文
ダメ出しも含めて、まずは問題文を掲載します。
2025年共通テスト 数学II,数学B,数学C
第5問
以下の問題を解答するにあたっては、必要に応じて31ページの正規分布表を用いてもよい。(正規分布表は省略)
Q地域ではレモンを栽培しており、収穫されるレモンを重さによってサイズごとに分類している(表1)。過去に収穫されたレモンの重さは、平均が110g、標準偏差が20gの正規分布に従うとする。表1
| サイズ | レモン1個の重さ |
| S | 80g以上90g未満 |
| M | 90g以上110g未満 |
| L | 110g以上140g未満 |
| 2L | 140g以上170g未満 |
| その他 | 80g未満または170g以上 |
(1)
Q地域で今年収穫されるレモンの重さ(単位はg)は、過去に収穫されたレモンの重さと同じ分布に従うとする。すなわち今年収穫される1個のレモンの重さを確率変数Xで表すと、Xは正規分布N(110,202)に従うとする。よって、今年収穫されるレモンから無作為にレモンを1個抽出する時、そのレモンがLサイズである確率は、P(110≦X<140) = P(110≦X≦140)であることに注意すると、
0.「アイウエ」である。
いま、Q地域で今年収穫されるレモンが20万個であるとし、その中のLサイズのレモンの個数を確率変数Yで表すと、Yは二項分布に従い、Yの平均(期待値)は「オ」になる。
(2)
太郎さんと花子さんは、Q地域で今年収穫されるレモンから何個か抽出して、今年収穫されるレモンの重さの平均(母平均)を推定する方法について話している。
太郎:母平均に対する信頼度95%の信頼区間の幅を4g以下にして推定したいね。
花子:母標準偏差を過去と同じ20gとすると、何個のレモンの重さを量ればいいかな。
太郎:信頼区間の式から、必要な標本の大きさを求めてみようよ。
母平均に対する信頼度95%の信頼区間の幅を4g以下にするために必要な標本の大きさを求める。いま、Q地域で今年収穫されるレモン全体を母集団とし、その重さの母平均をm g、母標準偏差をσ gとする。この母集団から無作為に抽出したn個のレモンの重さを確率変数W1,W2....Wnで表すと、標本の大きさnが十分に大きいとき、標本平均Wバー=1/n (W1+W2+....+Wn)は近似的に正規分布N(m,「カ」)に従う。またmに対する信頼度95%の信頼区間をA≦m≦Bと表すと、信頼区間の幅はB-A=「キ」/√n となる。
したがって、母標準偏差を過去と同じσ=20として、nに関する不等式
「キ」/√n<=4・・・・①
を満たす自然数nを求めればよい。①の両辺は正であるから両辺を2乗して整理すると「キ」2≦16n となる。この不等式を満たす最小の自然数nをnsとするとns=「クケコ」である。ゆえにmに対する信頼度95%の信頼区間の幅を4g以下にするために必要な標本の大きさnのうち、最小のものは「クケコ」であることが分かる。
(3)
太郎さんと花子さんは、Q地区で今年収穫されるレモンの重さについて話している。
太郎:今年のレモンの重さは、他の地域では例年よりも軽そうだと聞いたよ。
花子:Q地域でも、過去の平均110gと比べて軽いのかな。
太郎:標本の大きさを400、母標準偏差を過去と同じ20gとして、仮説検定ををしてみようよ。
(2)のmを用いて、Q地域で今年収穫されるレモンの重さの母平均mgが過去の平均110gより軽いといえるかを、有意水準5%(0.05)で仮説検定を行い検証したい。ただし、標本の大きさは400、母標準偏差は過去と同じ20gとする。
ここで、統計的に検証したい仮説を「対立仮説」、対立仮説に反する過程として設けた仮説を「帰無仮説」とする。このとき、帰無仮説は「m=110g」、対立仮説は「サ」である。これらの仮説に対して、有意水準5%で帰無仮説が棄却(否定)されるかどうかを判断する。
いま、帰無仮説が正しいと仮定する。標本の大きさ400は十分に大きいので、(2)の標本平均Wバーは、近似的に正規分布「シ」に従う。無作為抽出した400個のレモンの重さの平均が108.2gとなった。このとき、確率P(Wバー≦108.2g)は、0.「スセソタ」となる。この値をパーセント表示した値は有意水準5%より「チ」。したがって、有意水準5%で今年収穫されるレモンの大きさの母平均は110gより軽いと「ツ」。
(正規分布表、選択枝は省略)実際の正解については各予備校が公表しているので、そちらを参照してください。(手抜き)
Z検定の片側検定で誤差5%で有意差ありという答えになっています。
僕の記事を1から順番に読んできた方にはわかると思うけど、「今年のレモンの母分散が、去年と同じであると仮定」「正規分布を用いて片側5%で検定」、、、確かに400個もレモンを無作為に集めたら、殆どT分布は正規分布に近づきますが。共通テストでは許されるのかもしれませんが、もしこれが臨床研究・治験であったら、ほぼ確実にリジェクトされるでしょう。
得られた標本から不偏分散を計算すべきでしょう。そして、正規検定ではなく、T検定すべきですね。また片側検定を行う場合は有意水準は2.5%に設定することがガイドラインで示されています。詳しくは両側検定・片側検定の項を読んでください。
では、改めて、正しい統計処理を行ってみましょう。
この試験問題を一言で表現すると、「今年は20万個のレモンから400個のサンプルをとり、標本平均が108.2gだった。過去の実績では平均110g。標準偏差SD=20g。今年は不作の年なのか知りたい。」という問題になります。
2種類の過誤について
ちょっと面倒くさい話ですが、実際のデータと、標本に発生する過誤(エラー)について触れておきます。標本を無作為に正確に抽出するのは、本当に難しい作業です。また、最初に述べたように「木を見て森を想像している」訳なので、標本には一定の誤差が発生します。
| 2種類の過誤 | 真 実 | ||
| 真 | 偽 | ||
| 測定結果 | 真 | 〇 | 第2種の過誤 βエラー |
| 偽 | 第1種の過誤 αエラー | 〇 | |
真実で「真」のものを「偽」としてしまう:第1種の過誤(αエラー)
真実で「偽」のものを「真」としてしまう:第2種の過誤(βエラー)
と呼ばれています。
統計学的仮説検定では、証明したいことの逆の仮説である「帰無仮説」を設定し、帰無仮説の実現する確率が非常に低いことを示す。論理学の「背理法」を用いて証明します。
また、実験には一定の誤差があることを認め、その誤差を排除しても、差があると論理立てします。仮定を棄てる基準の確率を「有意水準」または「危険率」といい、少なくともαエラー5%以下でなければ、統計学的に有意とは言えません。(20回に1回、間違いを犯す)
(1-β)は検出力と言い、こちらも基準があります。(T検定では使いません。サンプルサイズの計算等で使います。)
詳しく知りたい方は、成書をご覧ください。(手抜き)
両側検定か、片側検定か
医学研究で平均値の差の検定(T検定等)を実施する場合は、原則として「両側検定」を行います。誤差は、平均値と比較しプラス側とマイナス側の何方にも発生しうるからです。なお片側検定よりも両側検定の方が厳しい条件になります。(有意になりにくい)「片側検定」が使えるのは、「理論的に片側にしか誤差が発生しえない明確な根拠がある場合のみ」です。(もちろんカイ二乗検定等、片側検定しか行えない検定法もあるので誤解のないように)
この入試問題では、例年のレモンの重さの平均値と、今年のレモンの重さの平均値を比較しています。レモンの重さは重くなる可能性も、軽くなる可能性もあります。両側検定を選択すべきでしょう。高校で教えている統計学だと正しいのでしょうが、レモンの重さの比較には、片側検定をして良い正当な理由が無いと思います。
なお、ICH E9(「臨床試験のための統計的原則」について)では、「片側検定をする場合には有意水準を2.5%とし、両側検定の場合には5%とすること」と明記されています。
T検定をしてみよう
本来なら、過去のレモンの重さと、今年のレモンの重さを比較しており、1群とは言い難い状況なのですが、与えられた問題では、昨年までのレモンの重さの平均値と分散値は示されていますが、今年のレモンのサンプルについては平均値しか示されておらず、今年のサンプルから算出された不偏分散が示されていません。これでは2群の比較ができません。
ということで、しかたなく、1群の平均値の比較としてT検定しましょう。(この試験問題では1群の正規検定をしているし。)
証明したい仮説は、英語では「alternative hypothesis」(直訳すると「選択仮説」)です。日本語では「対立仮説」という奇妙な名前になっています。帰無仮説は、英語では「null hypothesis」直訳すると「無の仮説」なので分かりやすいです。
「帰無仮説の反対の仮説」の意味でしょうけど、裏の裏は表といってるわけで。日本語訳が分かりにくい!ここも統計学の躓きポイントですね。 まぁ、昔の偉い人が命名したから、今更変更できないんでしょうけど・・・・・。
改めて問題を提示します。「20万個のレモンから、400個のサンプルをとり、標本平均が108.2gだった。標本標準偏差(母分散の予測値)SD=20g。過去の実績では平均110g。今年は不作の年なのか知りたい。」わけですね。証明したいのは「今年は不作かも」なので、帰無仮説は「今年の平均値の差は、5%の誤差範囲である」ですよね。レモンの重さは、過去の平均値より大きくなるか小さくなるか、両方の可能性があります。当然、誤差も両側に発生しえます。従って両側検定になります。
以下のtを計算し、両側5%(片側2.5%)で自由度399のT分布のX値t0.025(399)の値と比較します。
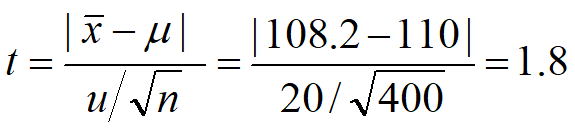
t0.025(399)≒t0.025(∞)=1.96 なので、計算されたtは、この値を超えていません。これでは有意な差とは言えないですね。
もし片側検定で有意水準5%なら、t0.05(399)< t0.05(240)=1.651であり、これを超えているので有意と言えるでしょうけどね。(t分布表の自由度の最大値は240であることが多いですね。)
検定手法の選択は、研究を始める前に、必ず統計の専門家の意見を聞きましょう!
論文を書くときに、どのような検定手法を使うべきかは、研究を始める前に専門家に相談しましょう。
データを集めた後に相談されても、「無理ですねぇ。」としか言えないです~。
まずは投稿したい雑誌で、自分の研究に類似した研究デザインのものを集めて、そこで使われている検定手法について研究しましょう。そしてダミーデータで検定試験を行い、実験が研究期間に完了可能かをシミュレーションしましょう!
例えば、お薬を投与する前と後で、平均値を比較する場合は、paired t-testも候補の1つです。前後の検体が、密接に結びついているからですね。ただし、T分布は母集団が正規分布していることが前提になります。正規分布していないと、ノンパラメトリック検定になります。
薬を投与した群と、偽薬を投与した群の平均値の比較である場合、「2群の平均値の比較」になります。
まずは「正規性の検定」を行い、どちらの群も正規分布していることを確認します。
次に、Leveneの検定かF検定を用いて「等分散であるか否かを検定」します。
等分散なら2群の差の検定T-testが使えます。最近は等分散であっても、より万全なWelch補正式を用いたt-testを推奨している方もいらっしゃいます。
等分散でないならWelchの補正が使うか、ノンパラメトリック検定になります。等分散でない場合のWelch補正については議論の余地があるので、確実性を優先するならノンパラメトリック検定を選択することになります。
ここで、「ノンパラメトリック検定したらいいんだ!」と安易に考えないでください。ノンパラメトリック検定で有意となるには相当なサンプル数と、明確な差が無いと無理です。多施設共同研究や大規模な創薬治験ならいざ知らず、学生が個人的な研究で集められる標本数で、ノンパラメトリック検定で有意になる可能性は「極めて低い」です。(仮にどれぐらいのサンプルが手に入って、どれくらいの差になりそうかを予測して、統計処理ソフトでシミュレーションしてみてください。研究を始める前にね!!)
ですから、卒論等、研究期間と予算に限りがある場合は、出来るだけパラメトリック検定で、可能ならT検定が使えるような研究デザインにすべきです。
論文を雑誌に投稿し、査読者からRejectされた場合に、まずは査読者の指示に従うのが鉄則ですが、全く聞き耳を持たない、一刀両断でRejectする方もいらっしゃいます。こういう時に「貴誌に掲載されている論文〇〇で、使われている統計手法と同様ですが、私の論文でその手法が使えない理由を教えていただきたい。」的な質問をする方法はあります。(査読者とは、絶対戦わない方が良い。どのように考えるべきか、教えを乞うスタイルがお勧めです。)
「あなたの論文は素晴らしいが、当雑誌の趣旨には合わないので、、、、」と言われたら、ほぼダメです。その雑誌は諦めましょう。😭
もし「どのように修正したら良いか」と質問して、大量の修正指示がでたら、「その通りに直せば採択される手応えあり!」です!
指導教官や統計の専門家に相談して、誠意を込めて修正しましょう。有名な雑誌だと4~5回はRejectされますよ。博士論文だと英語でのやりとりになります。頑張ろう!
次回は、統計処理ソフトRの使い方を説明しますね。Perl言語との連携にも触れます。